R - Binomial Distribution

The binomial distribution model deals with finding the probability of success of an event which has only two possible outcomes in a series of experiments. For example, tossing of a coin always gives a head or a tail. The probability of finding exactly 3 heads in tossing a coin repeatedly for 10 times is estimated during the binomial distribution.

R has four in-built functions to generate binomial distribution. They are described below.

dbinom(x, size, prob)
pbinom(x, size, prob)
qbinom(p, size, prob)
rbinom(n, size, prob)

Following is the description of the parameters used −

• x is a vector of numbers.
• p is a vector of probabilities.
• n is number of observations.
• size is the number of trials.
• prob is the probability of success of each trial.

dbinom()

This function gives the probability density distribution at each point.

# Create a sample of 50 numbers which are incremented by 1.
x <- seq(0,50,by = 1)

# Create the binomial distribution.
y <- dbinom(x,50,0.5)

# Give the chart file a name.
png(file = "dbinom.png")

# Plot the graph for this sample.
plot(x,y)

# Save the file.
dev.off()

When we execute the above code, it produces the following result −

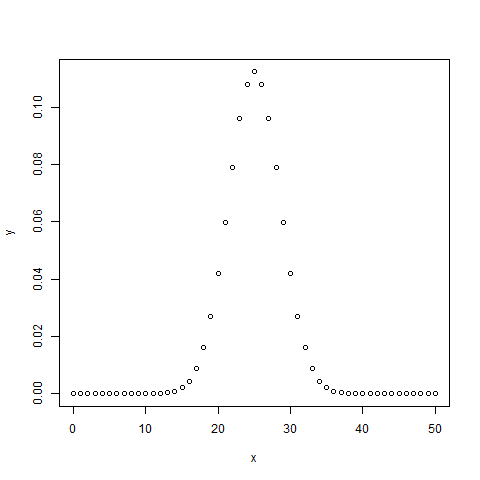
pbinom()

This function gives the cumulative probability of an event. It is a single value representing the probability.

# Probability of getting 26 or less heads from a 51 tosses of a coin.
x <- pbinom(26,51,0.5)

print(x)

When we execute the above code, it produces the following result −

[1] 0.610116

qbinom()

This function takes the probability value and gives a number whose cumulative value matches the probability value.

# How many heads will have a probability of 0.25 will come out when a coin
# is tossed 51 times.
x <- qbinom(0.25,51,1/2)

print(x)

When we execute the above code, it produces the following result −

[1] 23

rbinom()

This function generates required number of random values of given probability from a given sample.

# Find 8 random values from a sample of 150 with probability of 0.4.
x <- rbinom(8,150,.4)

print(x)

When we execute the above code, it produces the following result −

[1] 58 61 59 66 55 60 61 67